Вторая часть перевода лонгрида посвященного визуализации концепций из теории информации. Во второй части рассматриваются энтропия, перекрестная энтропия, дивергенция Кульбака-Лейблера, взаимная информация и дробные биты. Все концепции снабжены прекрасными визуальными объяснениями.
Для полноты восприятия, перед чтением второй части, рекомендую ознакомиться с первой.
Вычисление энтропии
Напомним, что стоимость сообщения длиной \(L\) равна \(\frac{1}{2^L}\). мы можем инвертировать это значение, чтобы получить длину сообщения, которое стоит заданную сумму: \(\log_2 (\frac{1}{cost})\). Поскольку мы тратим \(p(x)\) на кодовое слово для \(x\), длина будет равна \(\log_2(\frac{1}{p(x)})\). На рисунке выбор лучших длин кодовых слов.
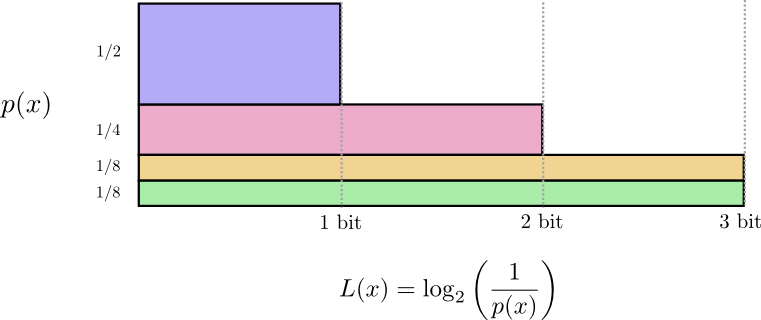
Ранее мы обсуждали, что существует фундаментальный предел того, насколько коротким может быть среднее сообщение для передачи событий из определенного распределения вероятностей \(p\). этот предел, средняя длина сообщения при использовании наилучшей системы кодирования, называется энтропией \(p, H(p)\). Теперь, когда мы знаем оптимальную длину кодовых слов, мы можем ее вычислить!
$$H(p)=\sum_xp(x)\log_2\Bigg(\frac{1}{p(x)}\Bigg)$$
(Часто энтропию записывают как \(H(p) = — \sum p(x)\log_2(p(x))\) используя равенство \(\log(1/a) = -\log(a)\). Мне кажется первая версия более интуитивна поэтому мы продолжим использовать ее.)
Если я хочу сообщить, какое событие произошло, то независимо от того, что я делаю, в среднем мне нужно отправить столько битов.
Среднее количество информации, необходимой для передачи чего-либо, имеет прямые следствия для сжатия. Но есть ли другие причины, по которым мы должны заботиться об этом? Да! Оно описывает мою неопределенность, и дает возможность количественно оценить информацию.
Если бы я знал наверняка, что произойдет, мне вообще не пришлось бы посылать сообщение! Если есть две вещи, которые могут произойти с вероятностью 50%, мне нужно отправить только 1 бит. Но если существует 64 различных события, которые могут произойти с одинаковой вероятностью, мне придется отправить 6 битов. Чем более концентрирована вероятность, тем больше у меня возможностей создать умный код с короткими средними сообщениями. Чем расплывчатее вероятность, тем длиннее должны быть мои сообщения.
Чем неопределеннее результат, тем больше я узнаю в среднем, когда мне сообщают о произошедшем.
Перекрестная энтропия
Незадолго до переезда в Австралию Боб женился на Алисе, тоже воображаемой. К моему удивлению, а также к удивлению других персонажей в моей голове, Алиса не была любительницей собак. Она была любительницей кошек. Несмотря на это, они смогли найти общий язык в своей общей одержимости животными и очень ограниченном словарном запасе.
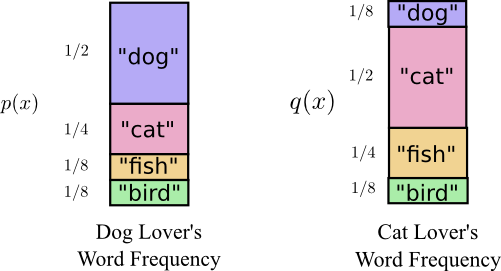
Эти двое используют одни и те же слова, только с разной частотой. Боб все время говорит о собаках, Алиса все время говорит о кошках.
Сначала Алиса посылала мне сообщения, используя код Боба. К сожалению, ее сообщения были длиннее, чем требовалось. Код Боба был оптимизирован под его распределение вероятностей. У Алисы другое распределение вероятностей, и код для нее неоптимален. Средняя длина кодового слова, когда Боб использует свой код, составляет 1,75 бита, когда же его использует Алиса, то 2,25. Было бы еще хуже, если бы эти двое не были так похожи!
Средняя длина сообщения из одного распределения с оптимальным кодом другого распределения называется перекрестной энтропией. Формально мы можем определить перекрестную энтропию следующим образом:
$$H_p(q)=\sum_xq(x)\log_2\Bigg(\frac{1}{p(x)}\Bigg)$$
В данном случае речь идет о перекрестной энтропии частоты слов кошатницы Алисы по отношению к частоте слов собачатника Боба.

Чтобы снизить стоимость нашей связи, я попросил Алису использовать ее собственный код. К моему облегчению, это снизило ее среднюю длину сообщения. Но это создавало новую проблему: иногда Боб случайно использовал код Алисы. Удивительно, но хуже когда Боб использует код Алисы, чем когда Алиса используют код Боба!
Итак, теперь у нас есть четыре возможности:
- Боб использует собственный код (\(H(p)=1.75\) бит)
- Алиса использует код Боба (\(H_p(q)=2.25\) бит)
- Алиса использует собственный код (\(H(q)=1.75\) бит)
- Боб использует код Алисы (\(H_q(p)=2.375\) бит)
Это не так интуитивно, как можно было бы подумать. Например, мы можем видеть, что \(H_p(q)≠H_q(p)\). Можем ли мы каким-то образом увидеть, как эти четыре значения соотносятся друг с другом?
На следующей диаграмме каждый подграфик представляет одну из этих 4 возможностей. Иллюстрации визуализируют среднюю длину сообщения. Они организованы в квадрат, так что, если сообщения из одного и того же распределения, диаграммы находятся рядом , а если они используют одни и те же коды, они находятся друг над другом. Это позволяет вам визуально совместить распределения и коды вместе.
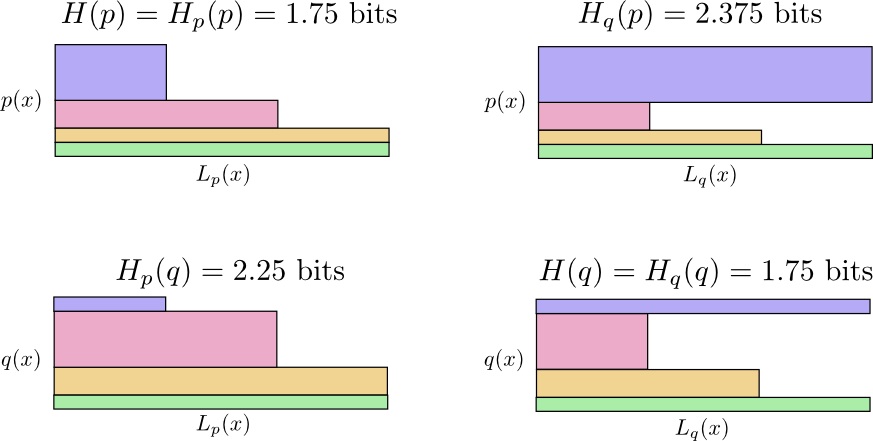
Видите почему \(H_p(q)≠H_q(p)\)? \(H_q(p)\) такой большой, потому событие отмеченное синим цветом часто встречается при \(p\), но получает длинное кодовое слово, потому что оно очень редко при \(q\). С другой стороны, частые события при \(q\) менее распространены при \(p\), но разница менее резкая, поэтому \(H_p(q)\) немного меньше.
Перекрестная энтропия не является симметричной.
Так, почему вас должна волновать перекрестная энтропия? Перекрестная энтропия дает нам способ выразить, насколько различны два распределения вероятностей. Чем сильнее отличаются распределения \(p\) и \(q\), тем больше перекрестная энтропия \(p\) относительно \(q\) будет больше энтропии \(p\).

Аналогично, чем больше \(q\) отличается от \(p\), тем больше перекрестная энтропия \(q\) относительно \(p\) будет больше энтропии \(q\).
По-настоящему интересной вещью является разница между энтропией и перекрестной энтропией. Эта разница равна тому насколько длиннее наши сообщения, потому что мы использовали код, оптимизированный для другого распределения. Если распределения одинаковы, то эта разница будет равна нулю. По мере того как отличия увеличиваются, она будет становиться больше.
Мы называем это различие дивергенцией Кульбака-Лейблера, или просто KL-дивергенцией. KL-дивергенция \(p\) относительно \(q\), \(D_q(p)\) определяется так:
$$D_q(p) = H_q(p) — H(p)$$
Самое замечательное в KL-дивергенции то, что она похожа на расстояние между двумя распределениями. Он измеряет, насколько они разные! (Если вы примете эту идею всерьез, вы придете к информационной геометрии.)
Перекрестная энтропия и KL-дивергенция невероятно полезны в машинном обучении. Часто мы хотим, чтобы одно распределение было близко к другому. Например, мы можем хотеть, чтобы предсказанное распределение было близко к основной истине. KL-дивергенция дает нам естественный способ сделать это, и поэтому она проявляется всюду.
Энтропия и несколько переменных
Давайте вернемся к нашему примеру с погодой и одеждой, приведенному ранее:
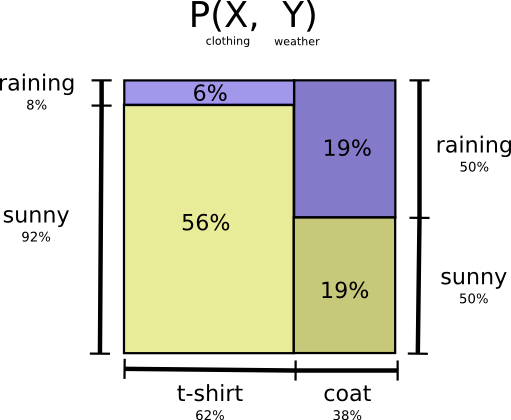
Моя мама, как и многие родители, иногда беспокоится, что я не одеваюсь соответственно погоде. (У нее есть веские основания для подозрений – я бывает не ношу плащ зимой.) Поэтому она часто хочет знать и погоду, и во что я одет. Сколько битов я должен послать ей, чтобы сообщить об этом?
Самый простой способ подумать об этом — выровнять распределение вероятностей:
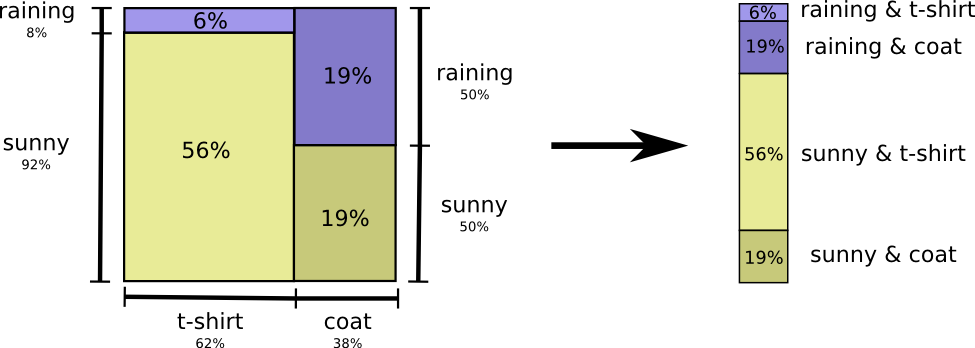
Теперь мы можем вычислить оптимальные кодовые слова для событий с такими вероятностями и вычислить среднюю длину сообщения:
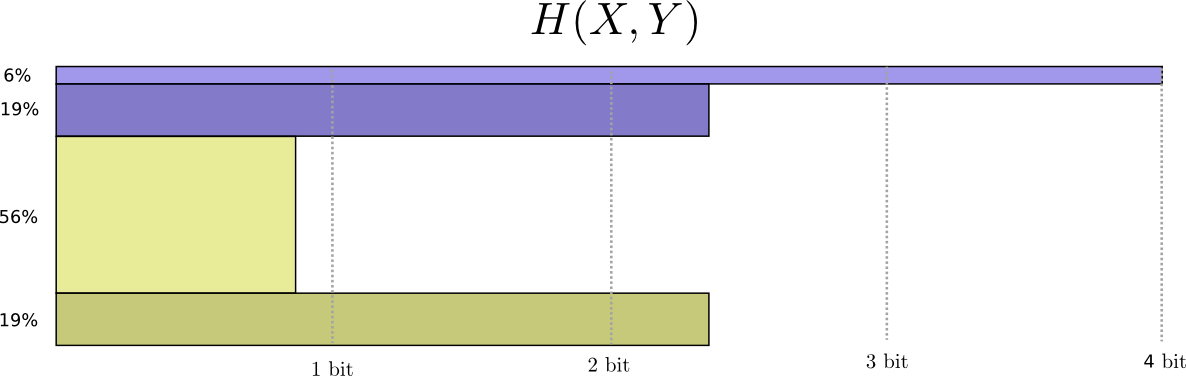
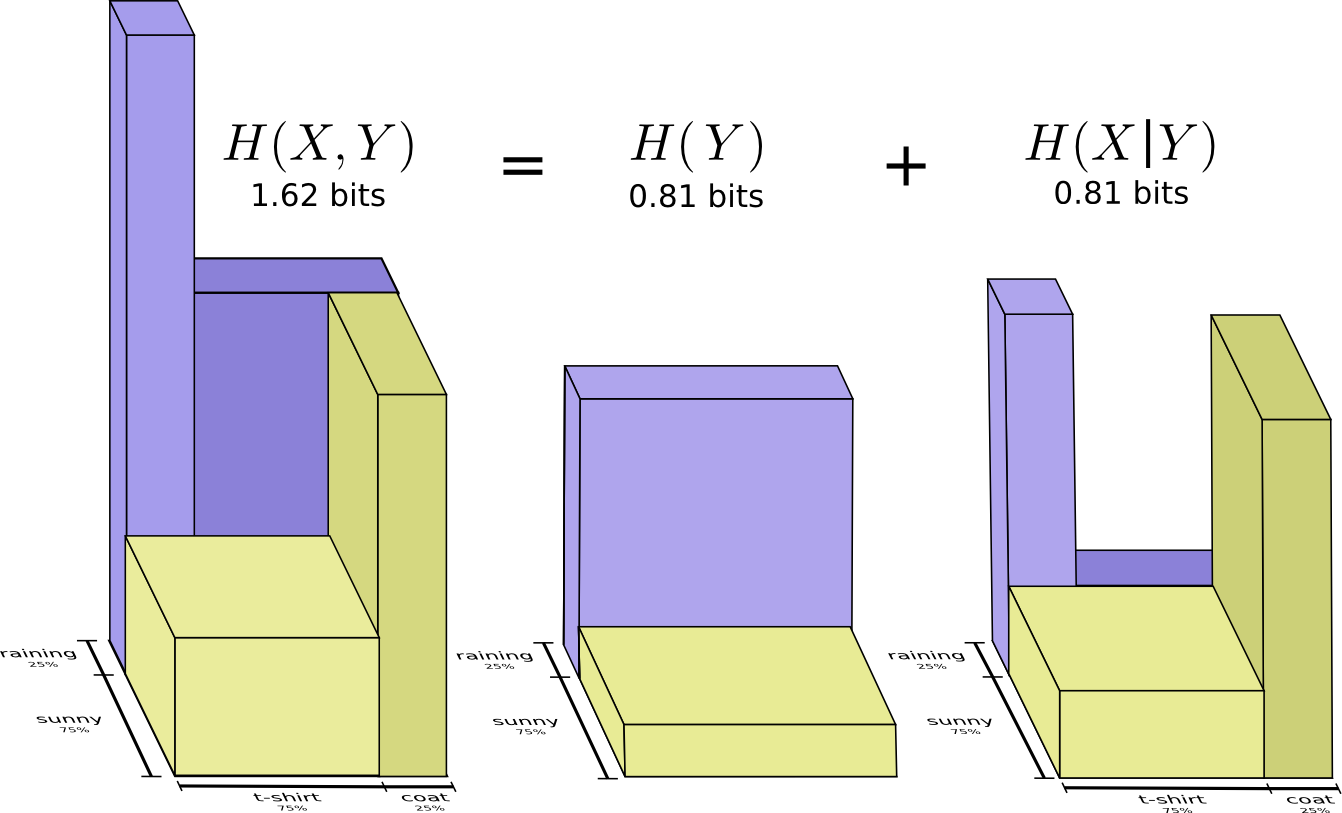
Мы называем это совместной энтропией \(X\) и \(Y\), определенной следующим образом:
$$H(X,Y)=\sum_{x,y}p(x,y)\log_2\bigg(\frac{1}{p(x,y)}\bigg)$$
Оно совпадает с нашим обычным определением, за исключением двух переменных вместо одной.
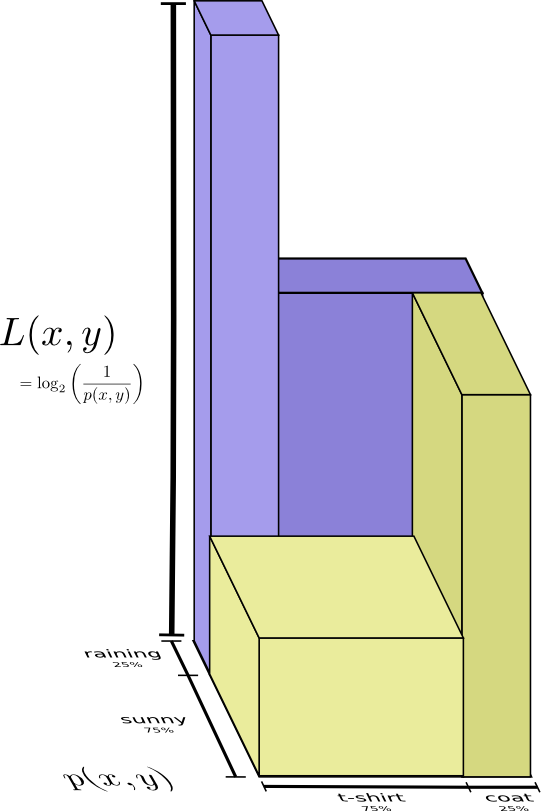
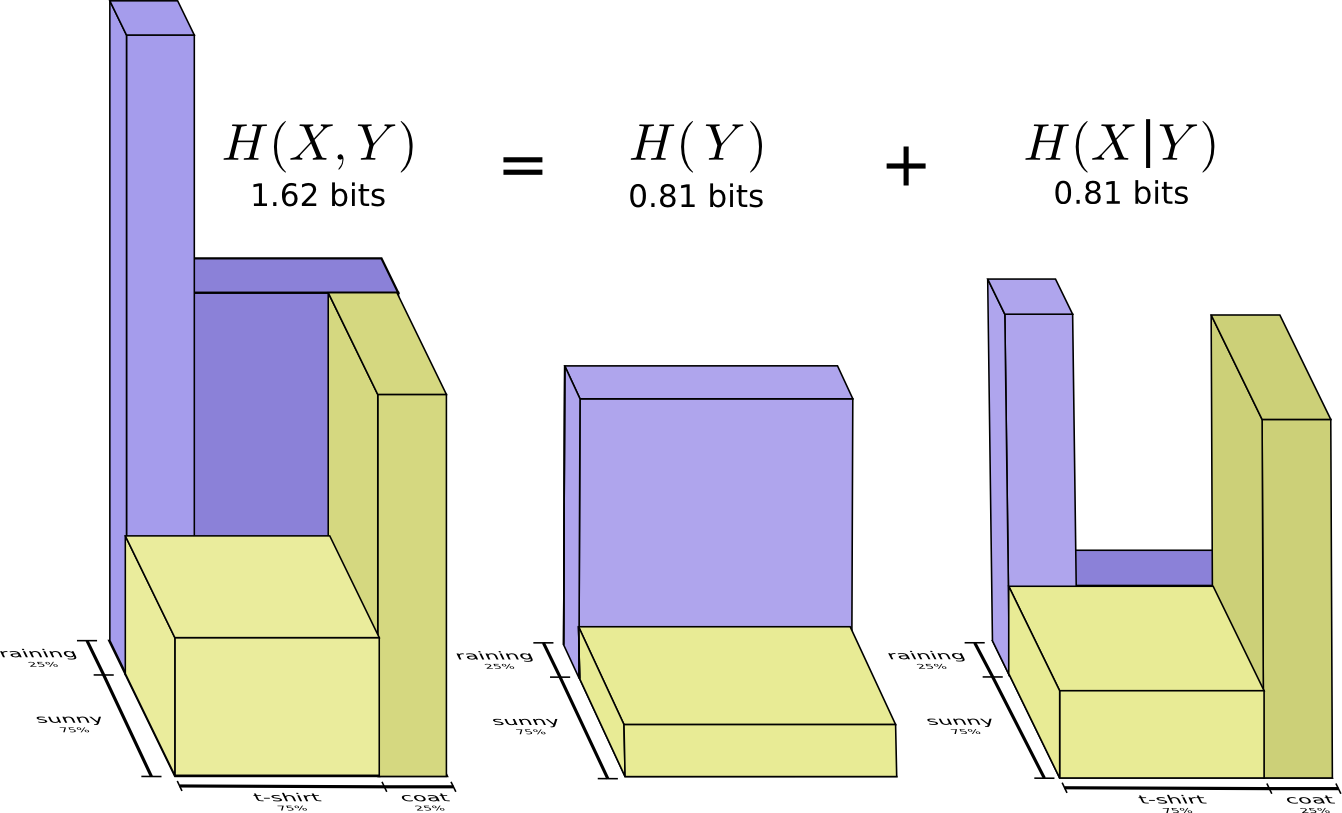
Немного лучший образ этого, без выравнивания распределения получается если представить длину кодового слова в третьем измерении. Теперь энтропия — это объем!
Но предположим, что моя мама уже знает погоду. Она может посмотреть ее в новостях. Сколько тогда информации мне нужно предоставить?
Похоже, мне нужно отправить информации достаточно, чтобы сообщить какая одежда на мне надета. Но на самом деле мне нужно посылать меньше информации, потому что от погоды сильно зависит то, какую одежду я надену! Давайте рассмотрим случай с дождем и с солнцем отдельно.
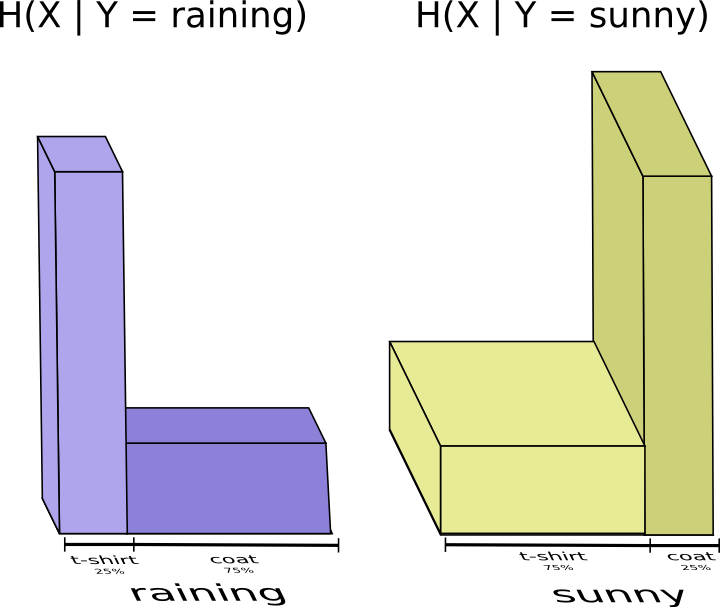
В обоих случаях мне не нужно посылать слишком много информации в среднем, потому что погода дает мне хорошее предположение о том, каким будет правильный ответ. Когда солнце, я могу использовать специальный оптимизированный для солнца код, а когда идет дождь, я могу использовать оптимизированный для дождя код. В обоих случаях я посылаю меньше информации, чем если бы я использовал общий код для обоих. Чтобы получить среднее количество информации, которое мне нужно отправить моей матери, я просто сложил эти два случая вместе…
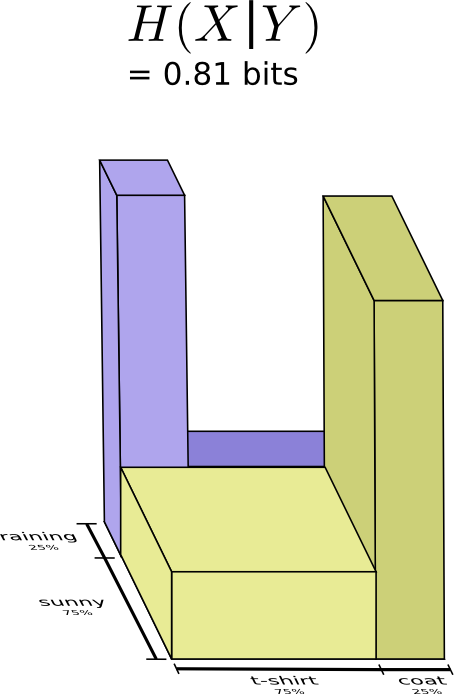
Мы называем это условной энтропией. Если вы формализуете его в уравнение, вы получаете:
$$H(X|Y)=\sum_yp(y)\sum_xp(x|y)\log_2\bigg(\frac{1}{p(x|y)}\bigg)$$
$$ =\sum_{x,y}p(x,y)\log_2\bigg(\frac{1}{p(x|y)}\bigg)$$
Взаимная информация
В предыдущем разделе мы выяснили, что знание одной переменной может означать, что для сообщения значения другой переменной требуется передать меньше информации.
Хороший способ думать об этом — это представить себе количество информации в виде полос. Эти полосы перекрываются, если между ними есть общая информация. Например, некоторая часть информации в \(X\) и \(Y\) общая, поэтому \(H(X)\) и \(H(Y)\) являются перекрывающимися полосами. И поскольку \(H(X,Y)\) — это информация обеих переменных, то это объединение полос \(H(X)\) и \(H(Y)\).
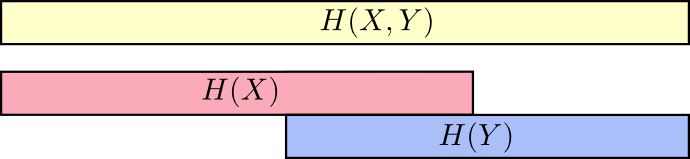
Когда мы думаем о вещах таким образом, многое становится проще увидеть.
Например, мы уже отмечали, что для передачи информации как \(X\), так и \(Y\) (“совместная энтропия”, \(H(X, Y)\)) требуется больше информации, чем для передачи только \(X\) (“предельная энтропия”, \(H(X)\)). Но если вы уже знаете \(Y\), то для передачи \(X\) (“условная энтропия”, \(H(X|Y)\)) требуется меньше информации, чем если бы вы этого не знали!
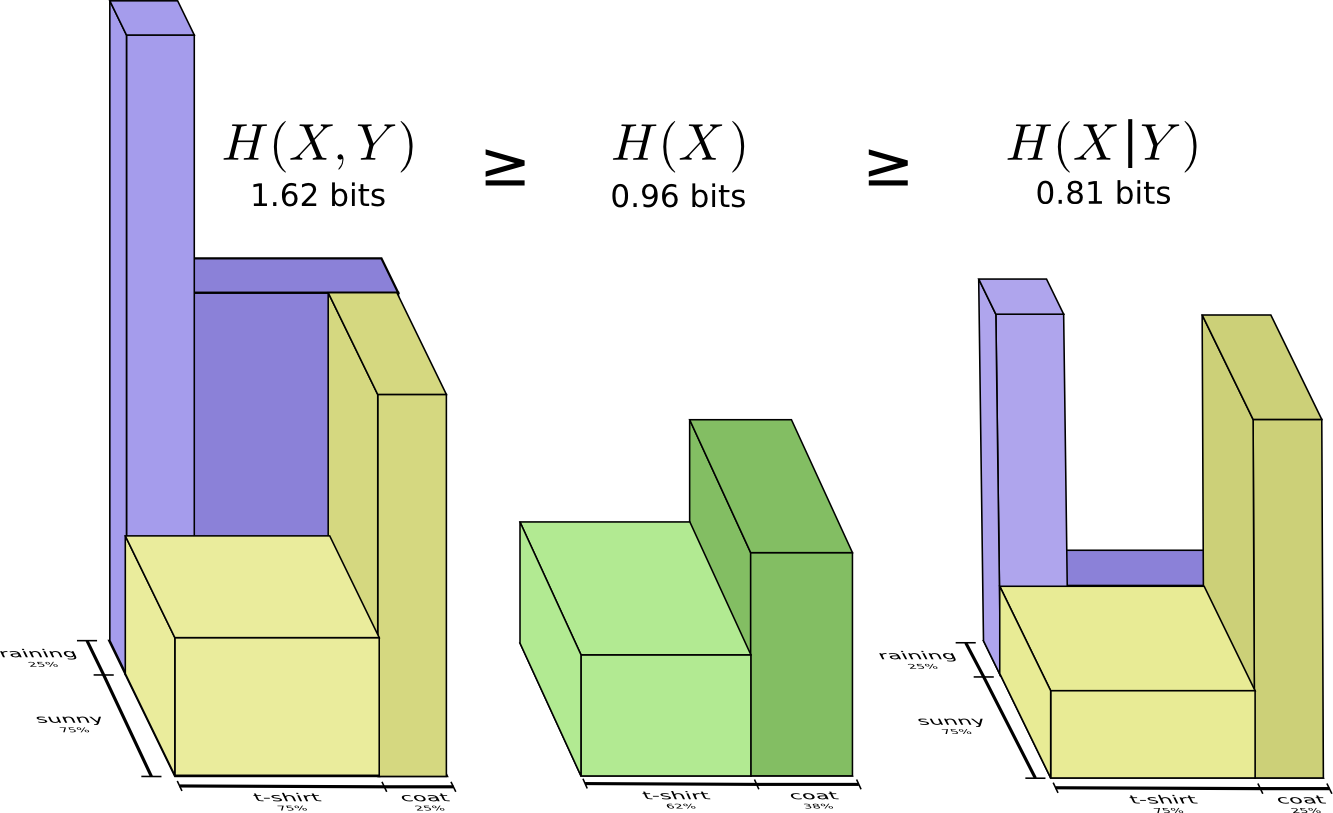
Это звучит сложновато, но если перевести на полосы то все оказывается очень просто. \(H(X|Y)\) — это информация, которую мы должны отправить, чтобы сообщить \(X\) тому, кто уже знает \(Y\), информация в \(X\), которая также не находится в \(Y\). Визуально это означает, что \(H(X|Y)\) — это часть полосы \(H(X)\), которая не перекрывается с \(H(Y)\).
Теперь вы можете прочитать неравенство \(H(X,Y)≥H(X)≥H(X|Y)\) прямо на следующей диаграмме.
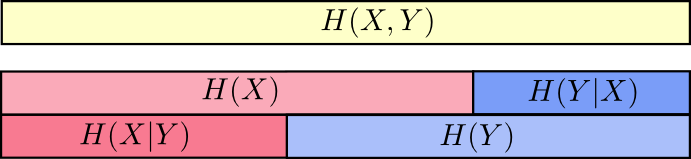
Другое равенство следующее — \(H(X,Y)=H(Y)+H(X|Y)\). Т.е. информация в \(X\) и \(Y\) это информация в \(Y\) плюс информация в \(X\) которой нет в \(Y\).
Опять же, это трудно увидеть в уравнениях, но легко увидеть, если вы думаете в терминах перекрывающихся полос информации.
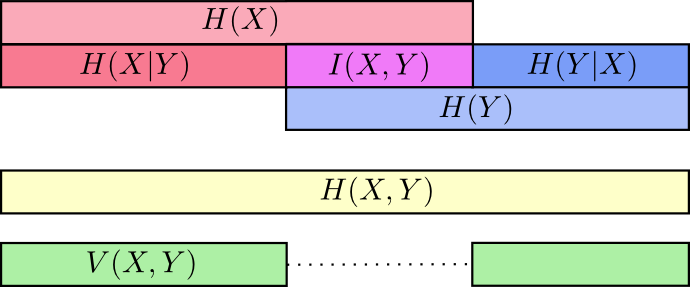
На этом этапе мы разбили информацию в \(X\) и \(Y\) несколькими способами. Мы знаем информацию в каждой переменной, \(H(X)\) и \(H(Y)\). Мы знаем объединение информации в обоих \(H(X,Y)\). У нас есть информация, которая находится в одной переменной, но отсутствует в другой, \(H(X|Y)\) и \(H(Y|X)\). Многое из этого, вращается вокруг информации, общей в переменных — пересечения их информации. Мы называем это «взаимной информацией», \(I(X, Y)\), определяемой как:
$$I(X,Y)=H(X)+H(Y)−H(X,Y)$$
Это определение верно, поскольку \(H(X)+H(Y)\) содержит две копии взаимной информации, так как она находится и в \(X\) и в \(Y\), в то время как \(H(X,Y)\) содержит только одну копию. (см. предыдущую диаграмму)
С взаимной информацией тесно связана вариация информации. Вариация информации — это информация, которая не является общей для переменных. Мы можем определить ее так:
$$V(X,Y)=H(X,Y)−I(X,Y)$$
Вариация информации интересна тем, что она дает нам метрику, понятие расстояния между различными переменными. Вариация информации между двумя переменными равна нулю, если знание значения одной переменной говорит вам о значении другой и становится больше по мере того, как они становятся более независимыми.
Как это соотносится с KL-дивергенцией, которая также дает нам понятие расстояния? KL-дивергенция это расстояние между двумя распределениями над одной и той же переменной или набору переменных. Напротив, вариация информации дает нам расстояние между двумя совместно распределенными переменными. KL дивергенция — это расхождение между распределениями, вариация информации внутри распределения.
Мы можем свести все это вместе в единую диаграмму, связывающую все эти различные виды информации:
Дробные биты
Очень неинтуитивной вещью в теории информации является то, что мы можем иметь дробные количества битов. Это довольно странно. Что значит половина бита?
Вот простой ответ: часто нас интересует средняя длина сообщения, а не длина какого-либо конкретного сообщения. Если в половине случаев посылается один бит, а в половине случаев — два, то в среднем посылается полтора бита. Нет ничего странного в том, что средние величины могут быть дробными.
Но этим ответом мы уклоняемся от вопроса. Часто оптимальные длины кодовых слов тоже являются дробными. Что это значит?
Чтобы быть конкретным, давайте рассмотрим распределение вероятностей, где одно событие, \(a\), происходит 71% времени, а другое событие, \(b\), происходит 29% времени.
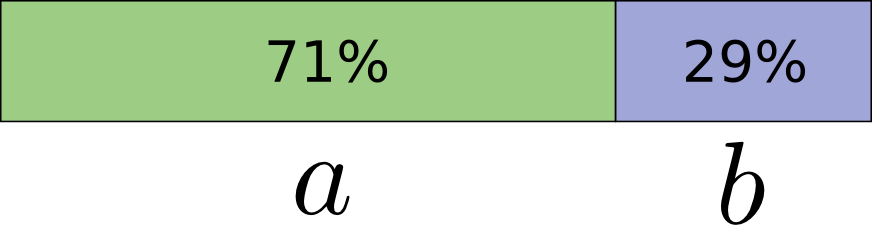
Оптимальный код будет использовать 0,5 бит для представления \(a\) и 1,7 бита для представления \(b\). Ну, если мы хотим отправить только одно из этих кодовых слов, такое представление невозможно. Мы вынуждены округлять до целого числа битов и отправлять в среднем 1 бит.
… Но если мы посылаем несколько сообщений одновременно, то оказывается можно сделать лучше. Давайте рассмотрим передачу двух событий из этого распределения. Если бы мы посылали их независимо, нам пришлось бы посылать два бита. Как нам это улучшить?

В половине случаев нам нужно посылать \(aa\), в 21% случаев — \(ab\) или \(ba\), а в 8% случаев — \(bb\). Опять же, идеальный код включает дробные количества битов.
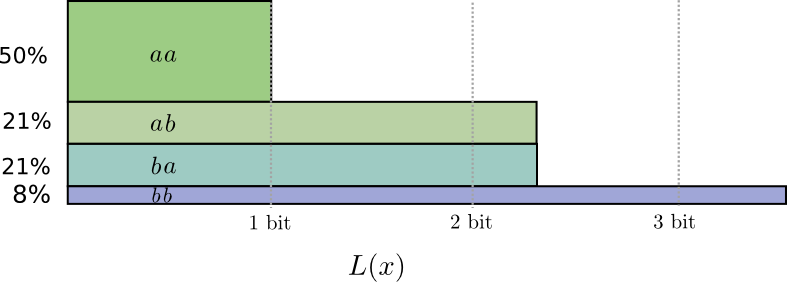
Если мы округлим длины кодовых слов, мы получим что-то вроде этого:
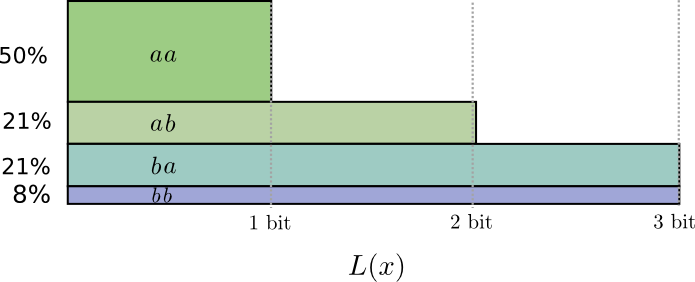
Эти коды дают нам среднюю длину сообщения 1,8 бит. Это меньше, чем 2 бита, когда мы посылаем сообщения независимо. Т.е. в этом случае мы посылаем 0,9 бит в среднем для каждого события. Если бы мы послали больше событий сразу, среднее значение стало бы еще меньше. При \(n\) стремящемся к бесконечности, накладные расходы, связанные с округлением нашего кода, исчезнут, и число битов на кодовое слово сойдется к энтропии.
Далее, обратите внимание, что идеальная длина кодового слова для события \(a\) составляла 0,5 бит, а идеальная длина для кодового слова \(aa\) — 1 бит. Идеальные длины кодовых слов складываются, даже если они дробные! Так что, если мы будем сообщать сразу несколько событий, длины будут складываться.
Как мы видим, существует реальный смысл, для дробные количеств битов информации, даже если фактические коды могут использовать только целые числа.
(На практике люди используют определенные схемы кодирования, которые эффективны в разных случаях. Код Хаффмана, который фактически является тем видом кода, который мы набросали здесь, не очень изящно обрабатывает дробные биты — вы должны группировать символы, как мы это делали выше, или использовать более сложные трюки, чтобы приблизиться к пределу энтропии. Арифметическое кодирование немного отличается, он элегантно обрабатывает дробные биты, чтобы быть асимптотически оптимальным.)
Заключение
Если нас волнует передача информации за минимальное количестве битов, то эти идеи, безусловно, фундаментальны. Если мы заботимся о сжатии данных, теория информации решает основные вопросы и дает нам фундаментально правильные абстракции. Но что, если нам все равно – разве это не экзотика?
Идеи из теории информации появляются во множестве контекстов: машинное обучение, квантовая физика, генетика, термодинамика и даже азартные игры. Практиков в этих областях теория информации заботит не потому, что они хотят сжать информацию. Их заботит то, что это имеет непреодолимую связь с их областью. Квантовую запутанность можно описать энтропией. Многие результаты в статистической механике и термодинамике можно получить, предположив максимальную энтропию о вещах, которых вы не знаете. Выигрыши и проигрыши игрока напрямую связаны с KL-дивергенцией в частности с итерационными сетапами (iterated setups).
Теория информации появляется во всех этих местах, потому что она предлагает конкретные, принципиальные формализации для многих вещей, которые мы должны выразить. Она дает нам способы измерения и выражения неопределенности, насколько различны два набора убеждений и что ответ на один вопрос говорит нам о других: насколько рассеяна вероятность, расстояние между распределениями вероятностей и насколько зависимы две переменные. Существуют ли альтернативные, подобные идеи? Конечно. Но идеи из теории информации чисты, они обладают действительно хорошими свойствами и основываются на принципах. В некоторых случаях эти идеи именно то, что вам нужно, а в других случаях они являются удобным посредником в хаотичном мире.
Машинное обучение — это то, что я знаю лучше всего, так что давайте поговорим об этом одну минуту. Очень распространенным видом задач в машинном обучении является классификация. Предположим, мы хотим посмотреть на картинку и предсказать, будет это изображение собаки или кошки. Наша модель может сказать что-то вроде: “есть 80% вероятности, что это изображение собаки, и 20% вероятности, что это кошка.» Допустим, правильный ответ — собака – насколько хорошо или плохо то, что мы сказали, что вероятность того что это собака 80%? Насколько лучше было бы сказать 85%?
Это важный вопрос, потому что нам нужно некоторое представление о том, насколько хороша или плоха наша модель, чтобы оптимизировать ее для достижения успеха. Что мы должны оптимизировать? Правильный ответ на самом деле зависит от того, для чего мы используем модель: заботимся ли мы только о том, была ли верна наша догадка, или нас волнует, насколько мы уверены в правильном ответе? Насколько это плохо — уверенно ошибаться? На это нет единственного правильного ответа. И часто невозможно узнать правильный ответ, потому что мы не знаем достаточно точно как будет использоваться модель, чтобы формализовать то, что нас в конечном счете волнует. Есть ситуации когда перекрестная энтропия — это именно то, что нас волнует, но это не всегда так. Гораздо чаще мы не знаем точно, что нас волнует, и перекрестная энтропия — действительно хороший прокси.
Информация дает нам сильную новую базу для размышления о мире. Иногда она идеально подходит для данной задачи; в других случаях не совсем, но все же чрезвычайно полезна. Это эссе только поскребло поверхность теории информации – есть основные темы, такие как коды исправления ошибок, которые мы вообще не касались, но я надеюсь, что я показал, что теория информации — это прекрасный предмет, который не должен быть пугающим.