Предлагаю вашему вниманию адаптированный перевод главы книги OnlineStatBook посвященной нормальным распределениям.
Вводный раздел определяет, что значит для распределения быть нормальным и представляет некоторые важные свойства нормального распределения. Интересная история открытия нормального распределения описана во втором разделе. Методы вычисления вероятностей, основанные на нормальном распределении, описаны в разделе «Области нормального распределения». «Разновидности нормального распределения» позволяет вам вводить значения среднего и стандартного отклонения нормального распределения и строить графики получившегося распределения. Часто используемое нормальное распределение, называемое стандартным нормальным распределением, описывается в одноименном разделе. Биномиальное распределение может быть аппроксимировано нормальным. Раздел «Нормальное приближение к биномиальному распределению» показывает это приближение. Демонстрация аппроксимации нормальным распределением позволяет вам исследовать точность этого приближения.
Введение
Нормальное распределение является наиболее важным и широко используемым распределением в статистике. Его иногда называют «колоколообразной кривой», хотя музыкальные качества такого колокола были бы не так приятны. Также его называют «распределением Гаусса» в честь математика Карла Фридриха Гаусса. Как вы увидите в разделе об истории нормального распределения, хотя Гаусс играл в ней важную роль, впервые обнаружил нормальное распределение Абрахам де Муавр.
Строго говоря, некорректно говорить о «нормальном распределении» поскольку существует много нормальных распределений. Нормальные распределения могут отличаться своими средними и стандартными отклонениями. На рис. 1 три нормальных распределения. У зеленого (самого левого) среднее равно -3, а стандартное отклонение 0.5, у красного распределения (посередине) среднее равно 0, а стандартное отклонение 1, и у черного распределение (справа) среднее равно 2 а стандартное отклонение 3. Эти, как и все другие нормальные распределения являются симметричными с относительно большими значениями в центре распределения и меньшими значениями в хвостах.

Плотность нормального распределения (высота для данного значения на оси x) показана ниже. Нормальное распределение определяется параметрами \(\mu\) и \(\sigma\) являющимися средним и стандартным отклонением соответственно. Символ \(e\) это основание натурального логарифма, а \(\pi\) это константа пи.
$$
\frac{1}{\sqrt{2\pi\sigma^2}} e^{\frac{-(x-\mu)^2}{2\sigma^2}}
$$
Поскольку мы не будем углубляться в математическую трактовку статистики, не беспокойтесь, если это выражение вас смущает. Мы не будем возвращаться к нему в следующих разделах.
Семь свойств нормального распределения указаны ниже. Эти свойства будут более подробно проиллюстрированы в следующих разделах этой главы.
- Нормальные распределения симметричны относительно своих средних.
- Среднее значение, мода и медиана нормального распределения совпадают.
- Площадь под нормальным распределением равна 1.
- Нормальные распределения плотнее в центре и менее плотны в хвостах.
- Нормальные распределения определяются двумя параметрами: среднее (m) и стандартное отклонение (s).
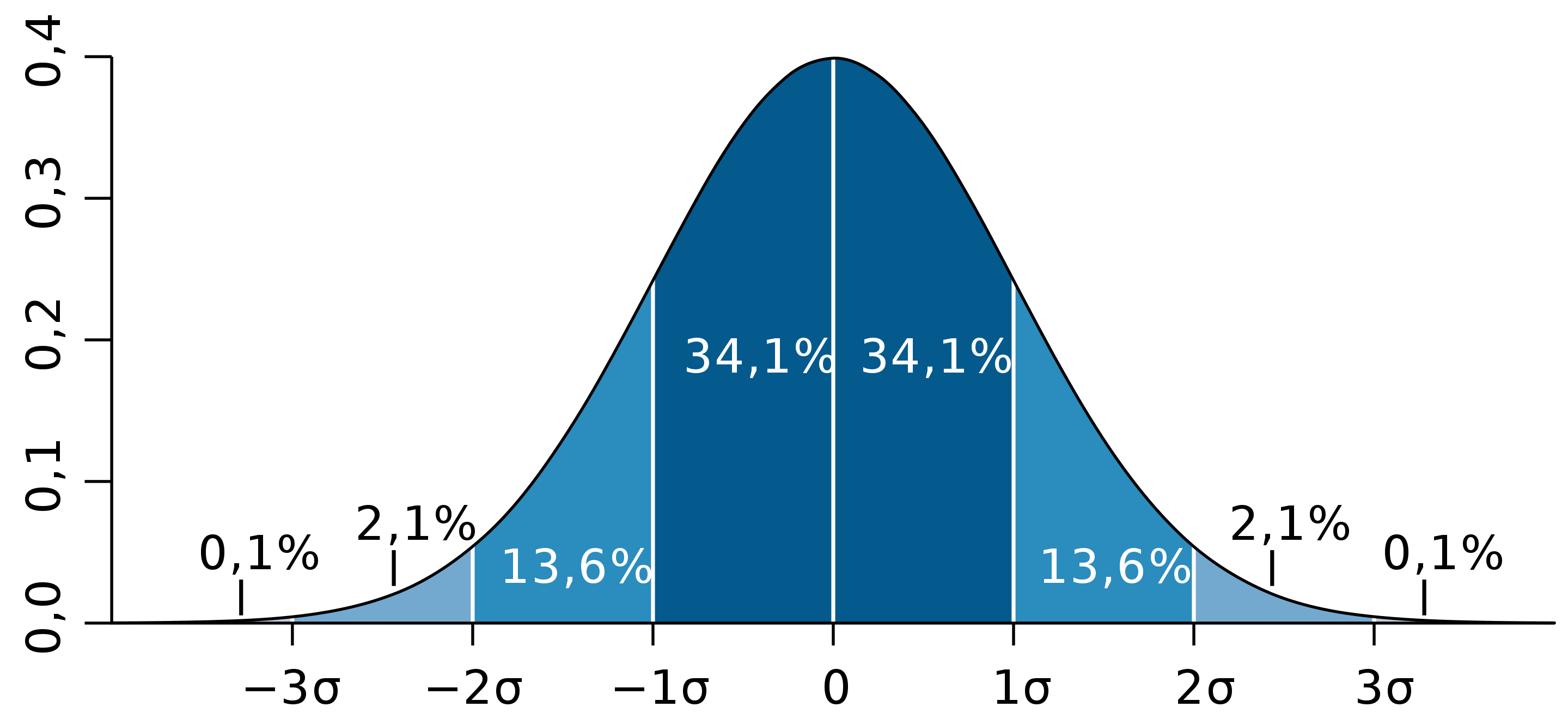
- 68% площади нормального распределения находится в пределах одного стандартного отклонения от среднего.
- Примерно 95% площади нормального распределения находится в пределах двух стандартных отклонений от среднего.
История нормального распределения
В главе посвященной вероятности мы увидели, что биномиальное распределение можно использовать для таких проблем, как: «Если подбросить честную монету 100 раз, какова вероятность выпадения 60 и более орлов?» Вероятность выпадения ровно x орлов за N подбрасываний рассчитывается по формуле:
$$
P(X) = \frac{N!}{x!(N-x!)}p^x(1-p)^{N-x}
$$
Где \(x\) это число орлов (60), \(N\) – количество подбрасываний монеты (100), а \(p\) это вероятность выпадения орла (0.5). Таким образом, чтобы решить эту проблему вам нужно вычислить вероятность 60 орлов, затем вероятность 61 орла, 62 и т.д. и сложить эти вероятности. Представьте, сколько времени потребовалось бы для вычисления биномиальных вероятностей до появления калькуляторов и компьютеров.
Абрахам де Муавр, статистик 18-го века и консультант азартных игроков, часто привлекался к проведению этих длительных вычислений. Де Муавр заметил, что, когда число событий (подбрасываний монет) увеличивается, форма биномиального распределения приближается к очень плавной кривой. Биномиальное распределение для 2, 4 и 12 подбрасываний показаны на рис. 2.

Де Муавр рассуждал, что, если бы он мог найти математическое выражение для этой кривой, он мог бы гораздо легче решать такие проблемы, как нахождение вероятности 60 и более орлов из 100 бросков монет. В точности это он и сделал, и кривая, которую он открыл, теперь называется «нормальной кривой».

Важность нормальной кривой обусловлена тем, что распределения многих природных явлений, по крайней мере приблизительно, нормально распределены. Одно из первых применений нормального распределения было к анализу ошибок измерений, сделанных при астрономических наблюдениях, ошибок произошедших из-за несовершенства инструментов и наблюдателей. Галилео в 17 веке отметил, что эти ошибки были симметричными и что небольшие ошибки возникали чаще, чем большие. Это привело к нескольким гипотезам о распределении ошибок, но только в начале 19-го века было установлено, что эти ошибки соответствуют нормальному распределению. Независимо друг от друга математики Адрейн в 1808 г. и Гаусс в 1809 г. разработали формулу для нормального распределения и показали, что ошибки хорошо соответствуют этому распределению.
Это же распределение было обнаружено Лапласом в 1778 г., когда он вывел чрезвычайно важную центральную предельную теорему, тему одного из следующих разделов. Лаплас показал, что даже если распределение не является нормальным, средние повторяющихся выборок из распределения будут распределены почти нормально, и чем больше размер выборки, тем ближе к нормальному будет распределение средних.
Большинство статистических процедур для проверки между средними значениями предполагают нормальное распределение. Поскольку распределение средних близко к нормальному, эти тесты работают хорошо даже если само распределение только приблизительно нормально. Кетле был первым, кто применил нормальное распределение к человеческим характеристикам. Он отметил, что такие характеристики, как рост, вес и сила были нормально распределены.
Площади нормального распределения
Площади под кусками нормального распределения могут быть вычислены с использованием математического анализа. Поскольку это нематематический подход к статистике, мы будем полагаться на компьютерные программы и таблицы для определения этих областей. На рис. 4 показано нормальное распределение со средним значением 50 и стандартным отклонением 10. Затененная область между 40 и 60 содержит 68% распределения.

На рис. 5 изображено нормальное распределение со средним равным 100 и стандартным отклонением 20. Как и на рис. 4, 68% распределения лежит в пределах одного стандартного отклонения от среднего.

Нормальные распределения показанные на рис. 4 и 5 это частные случаи общего правила о том, что 68% площади любого стандартного распределения находится в пределах одного стандартного отклонения от среднего.
На рис. 6 изображено нормальное распределение со средним 75 и стандартным отклонением 10. Закрашенная область содержит 95% площади и находится между 55.4 и 94.6. Для всех нормальных распределений 95% площади находится в пределах 1.96 стандартного отклонения. Для быстрых приближений иногда полезно округлять и использовать 2 вместо 1.96, в качестве числа стандартных отклонений, на которые вам нужно отступить от среднего, чтобы охватить 95% площади.

Для вычисления площадей под нормальным распределением может быть использован следующий нормальный калькулятор. Например, вы можете использовать его, чтобы найти пропорцию части нормального распределения со средним 90 и стандартным отклонением 12, которая больше 100. Установите среднее равным 90, стандартное отклонение – 12. Затем введите 110 в ячейку справа от кнопки «Above». Внизу экрана вы увидите, что закрашенная область равна 0.0478. Посмотрите сможете ли вы использовать калькулятор, чтобы узнать, что площадь между 115 и 120 равна 0.0124.

Скажем, вы хотите найти оценку, соответствующую 75-му перцентилю нормального распределения со средним значением 90 и стандартным отклонением 12. Используя обратный нормальный калькулятор, введите параметры, как показано на рис. 8, и обнаружьте, что площадь ниже 98.09 равна 0.75.

Стандартное нормальное распределение
Как обсуждалось во вводном разделе, у нормальных распределений не обязательно одинаковые средние и стандартные отклонения. Нормальное распределение со средним равным 0 и стандартным отклонением 1 называется стандартным нормальным распределением.
Области нормального распределения часто представлены таблицами стандартного нормального распределения. Часть таблицы стандартного нормального распределения показана в таблице 9.
| Z | Площадь под |
| -2.5 | 0.0062 |
| -2.49 | 0.0064 |
| -2.48 | 0.0066 |
| -2.47 | 0.0068 |
| -2.46 | 0.0069 |
| -2.45 | 0.0071 |
| -2.44 | 0.0073 |
| -2.43 | 0.0075 |
| -2.42 | 0.0078 |
| -2.41 | 0.008 |
| -2.4 | 0.0082 |
| -2.39 | 0.0084 |
| -2.38 | 0.0087 |
| -2.37 | 0.0089 |
| -2.36 | 0.0091 |
| -2.35 | 0.0094 |
| -2.34 | 0.0096 |
| -2.33 | 0.0099 |
| -2.32 | 0.0102 |
Первый столбец «Z» содержит значения стандартного нормального отклонения; второй столбец показывает значение площади левее Z. Поскольку среднее распределения равно нулю, а стандартное отклонение 1, в столбец Z равен числу стандартных отклонений левее (или правее) среднего значения. Например, Z равное -2.5 представляет значение равное 2.5 стандартных отклонений левее среднего. Площадь левее Z равна 0.0062.
Ту же информацию можно получить с помощью следующего калькулятора. На рис. 10 показано, как его можно использовать для вычисления площади левее значения -2,5 для стандартного нормального распределения. Обратите внимание, что среднее значение установлено на 0, а стандартное отклонение установлено на 1.

Значение из любого нормального распределения может быть преобразовано в соответствующее значение в стандартном нормальном распределении при помощи следующей формулы:
$$
Z = \frac{(X-\mu)}{\sigma}
$$
где \(Z\) это значение стандартного нормального распределения, \(X\) – значение исходного распределения, \(\mu\) — среднее исходного распределения, а \(\sigma\) — стандартное отклонение исходного распределения.
В качестве простого упражнения, какая часть нормального распределения со средним значением 50 и стандартным отклонением 10 меньше 26? Применяя формулу, получаем:
$$
Z = (26 – 50)/10 = -2.4
$$
Из таблицы 9, мы знаем, что 0.0082 распределения левее -2.4. Нет необходимости преобразовывать значение к \(Z\) если вы используете апплет как показано на рис. 11.

Если все значения распределения преобразовать в \(Z\) значения, то у распределения будет среднее 0 и стандартное отклонение 1. Процесс преобразования распределения к стандартному со средним 0 и отклонением 1 называется стандартизацией распределения.
Приближение биномиального распределения нормальным
В разделе об истории нормального распределения мы видели, что нормальное распределение можно использовать для аппроксимации биномиального распределения. В этом разделе показывается, как рассчитать эти приближения.
Давайте начнем с примера. Пусть у вас есть честная монета, и вы хотите знать вероятность выпадения 8 орлов за 10 бросков. У биномиального распределения есть среднее равное
\(\mu = Np = 10*0.5 = 5\) и дисперсия \(\sigma^2 = Np(1-p) = 10*0.5*05 = 2.5\). Стандартное отклонение при этом равно 1.5811. Результат 8 орлов равен \((8 — 5)/1.5811 = 1.897\) стандартных отклонений правее среднего распределения. «Какова вероятность получения значения в точности равного 1.897 стандартных отклонений правее среднего?» Вы можете удивиться, но ответ равен 0. Вероятность любой отдельной точки равна 0. Проблема в том, что биномиальное распределение является дискретным вероятностным распределением, тогда как нормальное распределение непрерывно.
Решение состоит в том, чтобы округлить и рассмотреть все значения от 7.5 до 8.5, для получения результат 8 орлов. Используя этот подход, мы вычисляем площадь под нормальной кривой от 7.5 до 8.5. Зона зеленого цвета на рис. 12 является приблизительной вероятностью получения 8 орлов.

Решение состоит в том, чтобы вычислить эту площадь. Сначала мы вычисляем площадь левее 8.5, а затем вычитаем из нее площадь левее 7,5.
Результаты использования калькулятора площади нормального распределения для определения области ниже 8.5 показаны на рисунке 13. Результаты для 7.5 показаны на рисунке 14.


Разница между площадями составляет 0.044, что является приближением биномиальной вероятности. Для этих параметров приближение очень точное.
Если у вас не было калькулятора площади нормального распределения, вы могли бы найти решение с помощью таблицы стандартного нормального распределения (таблица 9) следующим образом:
- Найти значение \(Z\) для 8.5, используя формулу \(Z = (8.5 — 5) / 1.5811 = 2.21\).
- Найти площадь левее \(Z\) равного 2.21 \(= 0,987\).
- Найти значение \(Z\) для 7.5, используя формулу \(Z = (7.5 — 5) / 1,5811 = 1.58\).
- Найти площадь левее \(Z\) 1.58 \(= 0.943\).
- Вычесть значение на шаге 4 из значения на шаге 2, и получить 0.044.
Та же логика применяется при расчете вероятности диапазона результатов. Например, чтобы рассчитать вероятность от 8 до 10 подбрасываний, вычислите площадь от 7.5 до 10.5.
Точность аппроксимации зависит от значений \(N\) и \(p\). Эмпирическое правило заключается в том, что аппроксимация хороша, если оба значения \(Np\) и \(N (1-p)\) больше 10.
Статистическая грамотность
Анализ рисков часто основан на предположении о нормальном распределении. Критики говорят, что экстремальные явления в действительности происходят чаще, чем можно было бы ожидать, если бы они были нормальными. Предположение даже было названо «большим интеллектуальным мошенничеством».
Недавняя статья, в которой обсуждается, как защитить инвестиции от экстремальных явлений, названных «риск хвоста» и определяемых как «риск хвоста, или экстремальный шок для финансовых рынков, технически определяется как инвестиция, которая двигается на более трех стандартных отклонений от среднего значения нормального распределения возврата инвестиций.»
Риск хвоста можно оценить, предполагая нормальность распределение и вычисляя вероятность такого события. Так ли следует оценивать «риск хвоста»?
События более трех стандартных отклонений от среднего значения очень редки для нормальных распределений. Однако они не так редки для других распределений, например с сильным перекосом. Если нормальное распределение используется для оценки вероятности событий хвоста, определенных таким образом, то «риск хвоста» будет недооценен.